Do you want to buy guest post to put backlink to your website? You can find list website that sells guest post here. List websites…
Code alteration or code modification is a malicious attempt as it can hamper the safety and security of the data and the software. Currently, many…
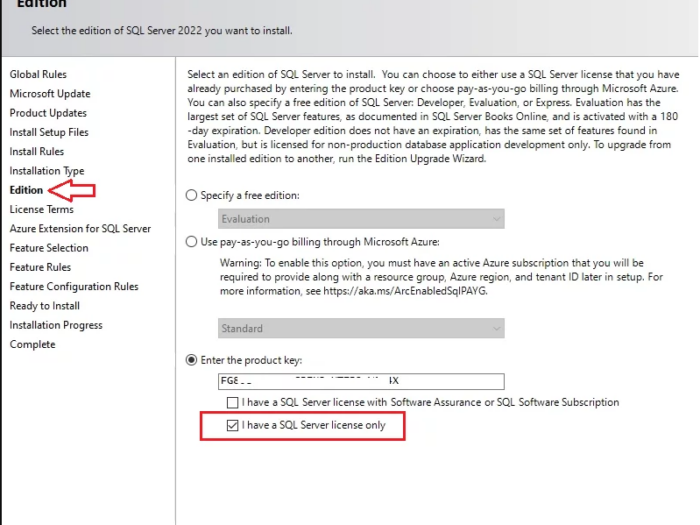
In this article I will guide you how to use SQL Server 2022 key and where you can buy SQL Server 2022 license key online…
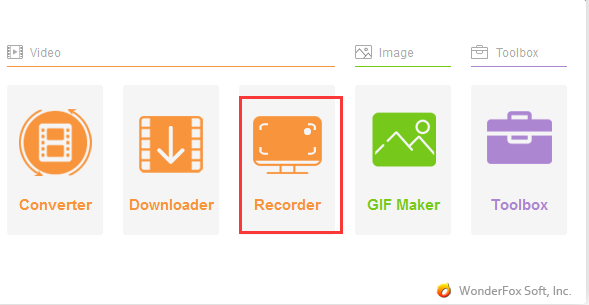
Windows 10 and Windows 11 have a built-in video capture feature called the Game Bar. With this function, you can easily capture screen content and…
Nowadays, global ransomware poses a serious risk to individual users, corporate organizations, and even government agencies. They continue to evolve and improve, adopting more complex…
With the development of multimedia production and broadcasting technology, more and more film and television works are produced based on high-definition, 4K or even 8K…
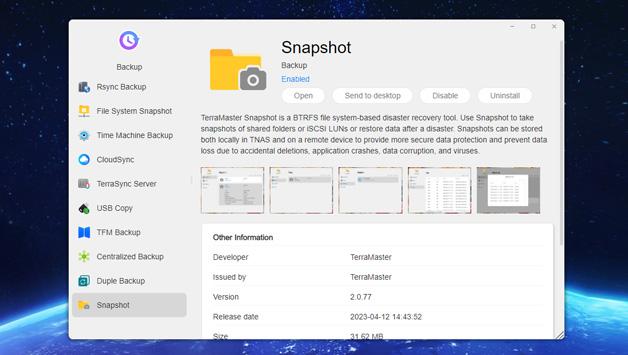
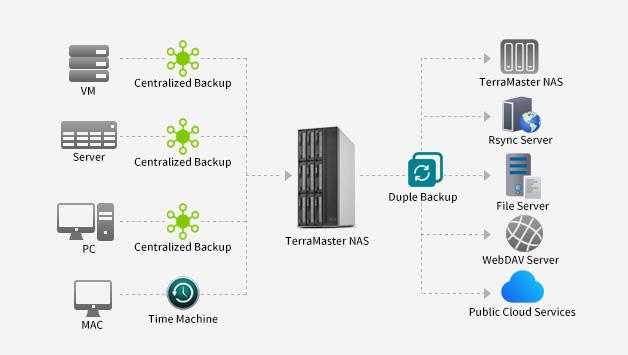
TerraMaster is professional brand that focuses on providing innovative storage products for homes and businesses. Nowadays, businesses face increasing data security challenges. Ensuring data integrity…
A User CAL (Client Access License) for Windows Server 2019 Remote Desktop Services allows one user to connect to a Remote Desktop Session Host server…
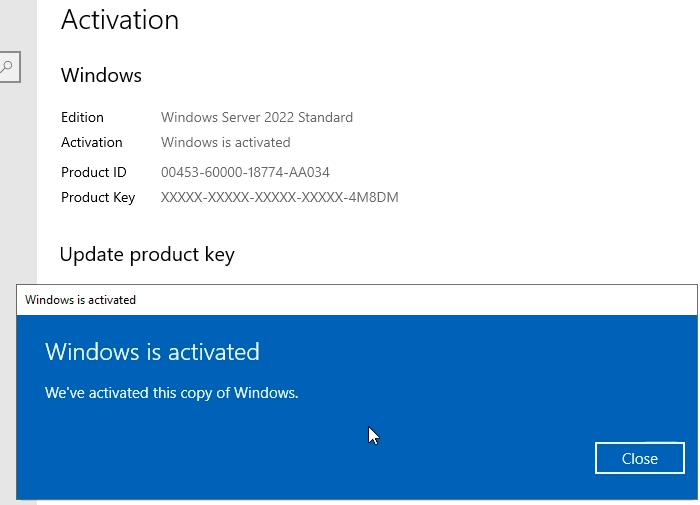
In this article I will give you Windows Server 2022 license key free and where to buy Windows Server 2022 retail key online with cheap…
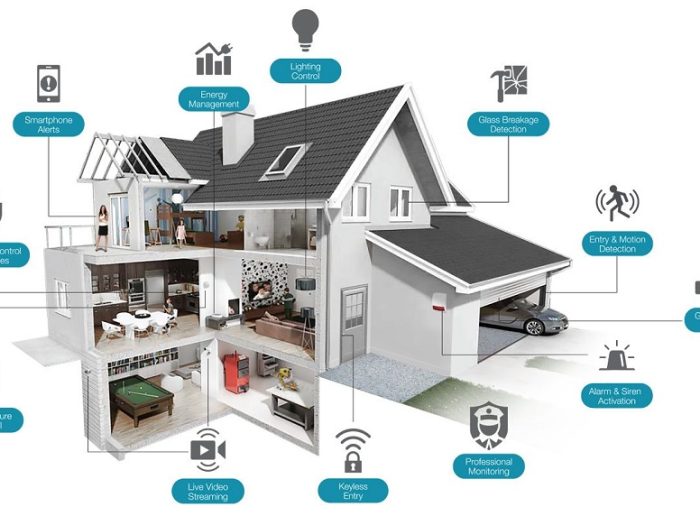
By and by we come across a new more horrifying than the last. Someone got robbed or mugged – the robber was armed … it…